THE CONCEPT OF SYMMETRY

Symmetry comes from a Greek word meaning 'to measure together' and is widely used in the study of geometry. Mathematically, symmetry means that one shape becomes exactly like another when you move it in some way: turn, flip or slide.

Symmetry has a more precise definition, that an object is invariant to any of various transformations; including reflection, rotation or scaling.

Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, theoretic models, language, music and even knowledge itself.

 Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that something does not change under a set of transformations. Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This occurs in many cases; for example, if X is a set with no additional structure,

 a symmetry is a bijective map from the set to itself, giving rise to permutation groups. If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (an isometry).

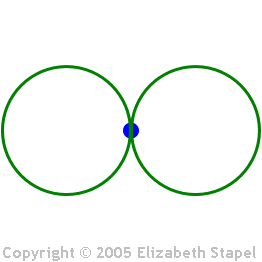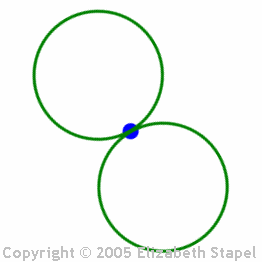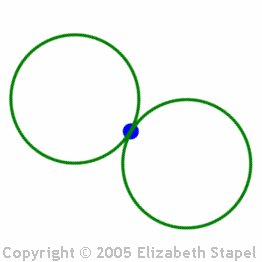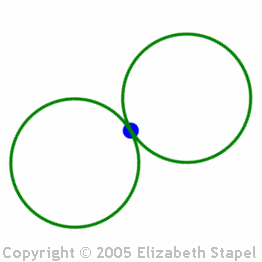
For instance, a figure-eight has a point of symmetry in the middle, where the lines cross

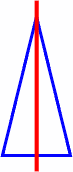
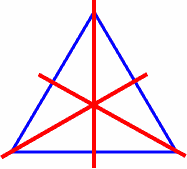
A triangle might have one or three lines of symmetry, but usually has none. For instance:

one line of symmetry:

three lines of symmetry:

no lines of symmetry:

And a circle has infinitely-many lines of symmetry, since any line through its center (that is, any diameter) is also an axis of symmetry.

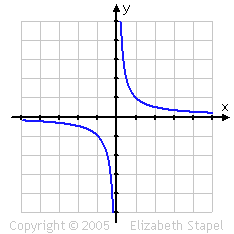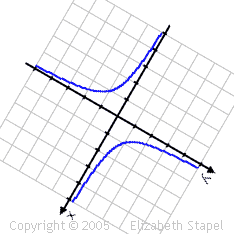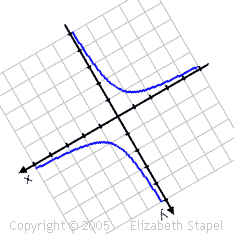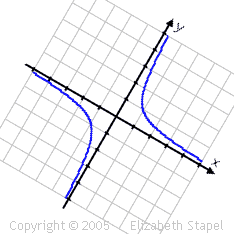
When working with symmetry about a line, you'll usually be asked for symmetry about an axis. With parabolas (and other conics), you may be asked for symmetry about any line. Either way, the concepts are the same, because:

The x-axis is just the line y = 0, and the y-axis is just the line x = 0.

Here are some examples of these types of symmetry:

The parabola y = x2 – 4 is shown below:

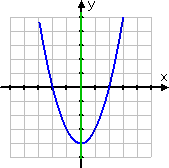
The line (or "axis") of symmetry is the y-axis, also known as the line x = 0. This line is marked green in the picture. The graph is said to be "symmetric about the y-axis", and this line of symmetry is also called the "axis of symmetry" for the parabola.

Contrary to the previous example, the parabola y = (x – 2)2 – 4 has a line (or axis) of symmetry, but is notsymmetric about either axis (that is, it is not symmetric about the x- or y-axis):

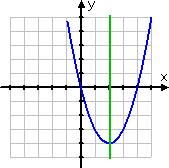
The axis here is the line x = 2, as marked in green above. If you were asked to "find the axis of symmetry for the parabola", you would answer "x = 2".

However, if you were asked, "Is the graph symmetric about either axis?", you would understand them to be asking only about symmetry about either the x- or y-axis; you would answer, "No."

Sometimes, you'll be asked about the symmetry of graphs which do not correspond to functions, but are actually relations. (That is, the graphs don't pass the Vertical Line Test.) Non-functional relations can have axes of symmetry. For instance, the graph of y2 = x + 4 is symmetric about the x-axis:

The axis of symmetry is the line y = 0, which is also the x-axis. If you were asked if this graph is symmetric about either axis, you would say, "Yes; about the x-axis." If you were asked for the axis of symmetry of the (sideways) parabola, you would say, "the line y = 0."

You can also view points of symmetry as being points about which you can rotate the shape 180° (with the resulting, rotated graph looking identical to the original graph), as shown below with the hyperbola:

...and the figure-eight:

By the way, don't let the preceding graphs fool you. The line of symmetry need not pass through or touch the graph of the underlying function or relation.